Bohr’s atomic model
In 1913, Neil Bohr proposed an atomic model to overcome the limitations of Rutherford’s atomic model of the atom. The postulates of Bohr’s atomic model are:
- Electrons revolve around the nucleus in a defined circular path called orbits. The electrostatic force of attraction between the revolving electron and nucleus is equal to the centrifugal force acting on the electron.
- As long as the atom remains in a particular orbit, it will neither gain nor lose energy and hence the energy of the electron in a particular orbit remains constant. This means these orbits are non-radiating and thus called stationary state or energy level and designated as K, L, M, N, etc.
- Only those orbits are permitted in an atom whose angular momentum of the electron is equal to the whole number multiple of h/2π where h is Plank’s constant.
Angular\ momentum\ (mvr) = \frac{nh}{2 \pi}\\ \begin {align*} where,\ m &= mass\ of\ electron\\ v &= velocity\ of\ electron\\ r &= radius\ of\ orbit\\ n &= 1,2,3,....\\ h &= Planck's\ constant = 6.67 \times 10^{-27} erg\ sec \end{align*}- Energy is emitted or absorbed by the electron in the form of a photon only when it jumps from one energy level to another. The quantum or photon of energy absorbed or emitted is the difference between the higher and lower energy level.
\Delta E = E_{2}-E_{1} = h\nu \\ \begin {align*} \Delta E &= energy\ emitted\ or\ absorbed\\ E_{2} &= higher\ energy\ level\\ E_{1} &= lower\ energy\ level\\ h &= Plank's\ constant\\ \nu &= frequency\ of\ radiation \end {align*}Energy is absorbed when an electron jumps from lower to higher energy level and energy is emitted when an electron jumps from higher to lower energy level.
Origin of hydrogen spectrum
When hydrogen gas is taken in a discharge tube and high voltage is applied, then there is the dissociation of hydrogen molecule into hydrogen atoms. Although hydrogen consists of only one electron, it produces different types of spectra. When energy is supplied, the electron of the hydrogen atom absorbs energy and jumps to a high energy level. The electrons in high energy level (excited state) are unstable and jump to lower energy level with the emission of electromagnetic radiation which give rise to line spectra called spectral series.
The equation to calculate the wavelength of different spectral series is:
\frac{1}{\lambda} = R\left [ \frac{1}{n_{1}^{2}}\ - \frac{1}{n_{2}^{2}}\ \right ]\\ \begin {align*} where, \lambda &= wavelength\\ R &= Rydberg\ constant\\ & n_{1}\ and\ n_{2}\ are\ energy\ level. \end{align*}Different types of spectral series are given below:
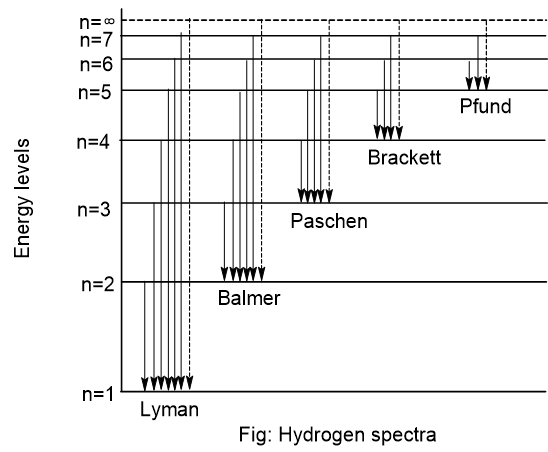
- Lyman series (92-120 nm):
It is observed when an electron jumps from a higher energy level to the first energy level. It lies in the ultraviolet region. - Balmer series (400-650 nm):
It is observed when an electron jumps from a higher energy level to a second energy level. It lies in the visible region. - Paschen series (950-1875 nm):
It is observed when an electron jumps from a higher energy level to a third energy level. It lies in the infrared region. - Brackett series (1945-4050 nm):
It is observed when an electron jumps from a higher energy level to a fourth energy level. It lies in the infrared region. - Pfund series (above 4050 nm):
It is observed when an electron jumps from a higher energy level to a fifth energy level. It lies in the infrared region.
Significances of Bohr’s atomic model
- It explains the stability of the atom.
- It explains the origin of line spectra of the hydrogen atom.
Limitations of Bohr’s atomic model
- No explanation for the multi-electron system:
This model only explained the origin of spectra of the hydrogen atom and hydrogen-like ions like He+, Li++, etc. but it doesn’t explain the origin of the spectra of the multielectron system. - No explanation of the hyperfine structure of spectra:
When the hydrogen spectra are observed with the help of a spectroscope of high resolving power, it is found that the individual spectral lines are not really single but consists of several closely packed lines called hyperfine lines. These fine lines cannot be explained by this model. Such structure means that in a given orbit, there are several orbits called sub orbits having different energies. - No explanation of Zeeman and Stark effect:
The splitting of spectral lines in presence of a magnetic field is called the Zeeman effect and the splitting of spectral lines in presence of an electric field is called the Stark effect. Bohr’s atomic model didn’t explain such effects. - No explanation for the dual nature of electron:
This model has treated electron as a particle of a certain mass revolving around the nucleus in a fixed orbit. But de-Broglie suggested that electron has a dual nature i. e. electron behaves as a particle as well as wave nature.
Dual nature of matter (de-Broglie equation)
In 1905, Einstein suggested the dual nature of light. According to this, light possesses a wave and particle nature. In 1924, de-Broglie advanced the idea that not only photons or light but also matter like electron shows the dual nature. The wave associated with matter is the matter wave or de-Broglie wave. So, the electron is a subatomic particle that can behave sometimes as a particle and sometimes as a wave.
The wave particle duality of matter led de-Broglie to derive the equation λ = h/P which indicates the wave and particle nature of the matter in motion.
Derivation
According to Planck’s quantum theory,
E = h\nu\ --- (i)\\ E=energy\ of\ photon,\\ h=Planck's\ constant\\ \nu=frequencyAccording to Einstein equation,
E = mc2 —- (ii)
m=mass, c=velocity of light
Combining eqn (i) and (ii),
\begin {align*} h\nu &= mc^{2}\\ or,\ h\frac{c}{\lambda} &= mc^{2} \ (\nu = c/\lambda\ and\ \lambda = wavelength)\\ or,\ \lambda &= \frac{h}{mv}\\ \lambda &= \frac{h}{P}\ (P\ is\ momentum\ and\ P=mv) \end{align*}It is de-Broglie wave equation. It shows that the momentum of a particle in motion is inversely proportional to its wavelength.
Significance
i. It shows the relation between particle and wave character of matter.
ii. It is applicable for all matter but more significant for microscopic particles like electron.
iii. It helps to deduce Bohr’s condition for quantization of angular momentum.
Differences between particle and wave
| Particle | Wave |
| A particle occupies a particular space. eg. a pen occupies a particular space. | A wave spreads in space. eg. sound of mike reaches everywhere. |
| No two or more particles occupy the same space at the same time. | Two or more wave co-exists in the same region at the same time. |
| When many particles are in space, the total volume is equal to the sum of their volume. | When many waves are present, the resultant wave can be greater or smaller than each individual wave. |


